Comme d'autres l'ont souligné, il est difficile de savoir ce qu'il voulait dire. Souvenez-vous qu'il rapportait quelque chose qui lui avait été dit et qu'il n'avait probablement pas entièrement compris à l'époque, ou dont il n'avait qu'un souvenir inexact au moment de la rédaction.

Cette réponse est la configuration cela m'est venu à l'esprit comme ayant une chance d'être celui qu'il avait en tête. (S'il ne l'avait pas en tête mais qu'on ne lui en avait parlé qu'à un moment donné, alors je m'attends à ce que l'exemple soit plus compliqué que le mien.)

Quand Newman écrit «qui sont capables de diviser un espace», je suppose que l'espace peut être le plan euclidien; il aurait écrit l'espace s'il avait voulu dire l'espace tridimensionnel. Je suppose donc qu'un crayon hyperbolique de cercles (l'ensemble de cercles bleus dans le dessin en est un échantillon fini):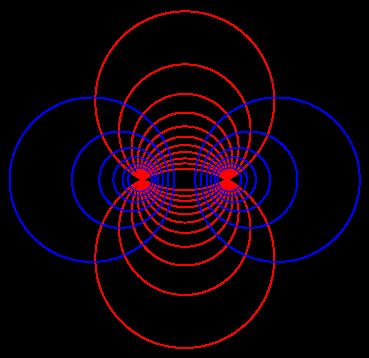

L'ensemble des cercles bleus, y compris la ligne droite verticale qui manque au milieu du dessin, contient une infinité de courbes. Si vous choisissez un nombre infiniment infini de (ou un nombre fini) d'entre eux, y compris la ligne droite de sorte que les tailles des cercles des deux côtés soient illimitées (ce qui signifie également qu'il y en a un arbitrairement près de la ligne droite de chaque côté), alors ces lignes partitionnent le plan ('diviser un espace') en formes de telle sorte qu'aucune de ces formes ne contienne une ligne droite.

Addendum. Un plus simple (mais équivalent, comme nous le verrons) exemple est un ensemble illimité de cercles concentriques et les anneaux concentriques définis par eux, par exemple à espacement égal: $$ \ Big \ {\ {x \ in \ mathbb {R} ^ 2 \, | \, n< | x | <n + 1 \} \ \ Big | \ n \ in \ mathbb {N} \ Gros \}. $$ Ceci est projectivement isomorphe pour mon premier exemple car il y a une transformation Möbius qui mappe une configuration à l'autre. Vous pouvez mapper

• les deux foyers ( points limites) du crayon de cercles, et le point où la ligne verticale coupe le segment entre les deux foyers

à

• le centre des cercles concentriques, à $ \ infty $, et à un point arbitraire de n'importe quel cercle de l'ensemble des cercles concentriques, respectivement.

Comparez avec ceci:

Une famille de cercles concentriques centrés sur un seul foyer C forme un cas particulier de crayon hyperbolique, dans lequel l'autre foyer est le point à l'infini de la ligne projective complexe. Le crayon elliptique correspondant est constitué de la famille des lignes droites passant par C; ceux-ci doivent être interprétés comme des cercles qui passent tous par le point à l'infini. ( Crayons de cercles, Wikipédia)